Making inference using data plots, with application to ecological statistics

Di Cook
Monash University

vISEC
June 24, 2020

https://dicook.org/files/vISEC2020/slides.html
Image credit: Di Cook, 2018

1 / 45

Data plots are utilised widely in ecology, often to make decisions. They can and should be integrated into the classical statistics infrastructure.2 / 45

I'm going to talk about

3 / 45

I'm going to talk about

inference for data plots

3 / 45

I'm going to talk about

inference for data plots

a high-throughput analysis

3 / 45

I'm going to talk about

inference for data plots

a high-throughput analysis

and computer vision experiments,

3 / 45

Inference for data plots requiresthe plot is a statistic 
4 / 45

Inference for data plots requiresthe plot is a statistic 
the type of plot (specified by a grammar) implicitly defines the null hypothesis
4 / 45

Inference for data plots requiresthe plot is a statistic 
the type of plot (specified by a grammar) implicitly defines the null hypothesis
a null generating mechanism provides draws from the sampling distribution, among which to embed the data plot
4 / 45

Inference for data plots requiresthe plot is a statistic 
the type of plot (specified by a grammar) implicitly defines the null hypothesis
a null generating mechanism provides draws from the sampling distribution, among which to embed the data plot
human (computer) observers are engaged to conduct a lineup test
4 / 45

Inference for data plots requiresthe plot is a statistic 
the type of plot (specified by a grammar) implicitly defines the null hypothesis
a null generating mechanism provides draws from the sampling distribution, among which to embed the data plot
human (computer) observers are engaged to conduct a lineup test
statistical significance and power can be computed based on the proportion of observers choosing the data plot from the lineup
4 / 45

Why is a plot a statistic?

Many of you (hopefully) use ggplot2 to make your plots with a grammar of graphics.

ggplot(data=DATA) + 
  geom_something(
    mapping=aes(x=VAR1, y=VAR2, colour=VAR3)
  ) +
  extra nice styling

5 / 45

Why is a plot a statistic?

Many of you (hopefully) use ggplot2 to make your plots with a grammar of graphics.

ggplot(data=DATA) + 
  geom_something(
    mapping=aes(x=VAR1, y=VAR2, colour=VAR3)
  ) +
  extra nice styling

A statistic is a function of a random variable(s). This is how the mapping can be interpreted.

5 / 45

Adding data gives a visual statistic

# Get some data
library(amt)
data("deer")
data("sh_forest")
rsf1 <- deer %>% random_points(n=1500) %>% 
  extract_covariates(sh_forest) %>% 
  mutate(forest = sh.forest == 1) %>%
  rename(x=x_, y=y_, sighted=case_)
# Plot it
ggplot(data=rsf1) +
  geom_point(
    aes(x=x, y=y, colour=sighted),
    alpha=0.7) +
  extra nice styling

Observed value of the statistic

6 / 45

ggplot(rsf1) +
  geom_bar(
    aes(x=sighted, fill=forest),
    position = "fill") + 
  extra nice styling

For sighted vs forest habitat the mapping requires call to stat=count:

## # A tibble: 4 x 3
## # Groups:   sighted [2]
##   sighted forest count
##   <lgl>   <lgl>  <int>
## 1 FALSE   FALSE   1188
## 2 FALSE   TRUE     312
## 3 TRUE    FALSE    560
## 4 TRUE    TRUE     266

Observed value of statistic

7 / 45

Null generating mechanism: Example 1

What's the null? What would be uninteresting?

ggplot(DATA) + 
  geom_POINT(
    aes(x=x, y=y, colour=sighted),
    alpha=0.7) +
  extra nice styling

8 / 45

Null generating mechanism: Example 1

What's the null? What would be uninteresting?

ggplot(DATA) + 
  geom_POINT(
    aes(x=x, y=y, colour=sighted),
    alpha=0.7) +
  extra nice styling

$H_{o} :$ Sightings are uniformly distributed in space

$H_{a} :$ Sightings are NOT uniformly distributed in space

Null generating mechanism could be to permute the labels of sighted variable. (Or could simulated a second uniform set of points.)

8 / 45

Null generating mechanism: Example 2

What's the null? What would be uninteresting?

ggplot(DATA) + 
  geom_BAR(
    aes(x=sighted, fill=forest),
    position = "fill") + 
  extra nice styling

9 / 45

Null generating mechanism: Example 2

What's the null? What would be uninteresting?

ggplot(DATA) + 
  geom_BAR(
    aes(x=sighted, fill=forest),
    position = "fill") + 
  extra nice styling

$H_{o} :$ No relationship between sighted and forest habitat

$H_{a} :$ Sightings in forest habitat more likely

Null generating mechanism could also be permute the labels of sighted (or forest) variable. (Or could simulate from a binomial.)

9 / 45

Pretend you haven't seen the data plot10 / 45

Which plot is different from the rest?

set.seed(20200624)
library(nullabor)
l <- lineup(null_permute("sighted"),
            rsf1, n=6)
ggplot(l) + 
  geom_point(
    aes(x=x, y=y, colour=sighted),  
    alpha=0.3) +
  facet_wrap(~.sample, ncol=2) + 
  extra nice styling

11 / 45

Which plot is different from the rest?

set.seed(20200624)
library(nullabor)
l <- lineup(null_permute("sighted"),
            rsf1, n=6)
ggplot(l) + 
  geom_point(
    aes(x=x, y=y, colour=sighted),  
    alpha=0.3) +
  facet_wrap(~.sample, ncol=2) + 
  extra nice styling

You say 1? Oh, that is the data plot.

11 / 45

set.seed(20200625)
l <- lineup(null_permute("sighted"),
            rsf1, n=9)
ggplot(l) +
  geom_bar(
    aes(x=sighted, fill=forest), 
    position = "fill") + 
  facet_wrap(~.sample, ncol=3) + 
  extra nice styling

In which plot is the light brown bar on the right the tallest?

12 / 45

set.seed(20200625)
l <- lineup(null_permute("sighted"),
            rsf1, n=9)
ggplot(l) +
  geom_bar(
    aes(x=sighted, fill=forest), 
    position = "fill") + 
  facet_wrap(~.sample, ncol=3) + 
  extra nice styling

In which plot is the light brown bar on the right the tallest?

Did you say 5? You're good!

12 / 45

In each case, the data plot was identifiable, and the null hypothesis would be rejected13 / 45

Inference for graphics infrastructure14 / 45

15 / 45

Visual inference broadens the scope of statistics16 / 45

Let's do a real lineup test17 / 45

Lineup protocol

I'm going to show you a page of plots

18 / 45

Lineup protocol

I'm going to show you a page of plots

Each has a number above it, this is its id

18 / 45

Lineup protocol

I'm going to show you a page of plots

Each has a number above it, this is its id

Choose the plot that you think exhibits the most separation between groups

18 / 45

Lineup protocol

I'm going to show you a page of plots

Each has a number above it, this is its id

Choose the plot that you think exhibits the most separation between groups

If you really need to choose more than one, or even not choose any, that is ok, too

18 / 45

Lineup protocol

I'm going to show you a page of plots

Each has a number above it, this is its id

Choose the plot that you think exhibits the most separation between groups

If you really need to choose more than one, or even not choose any, that is ok, too

Ready?

18 / 45

01:00

19 / 45

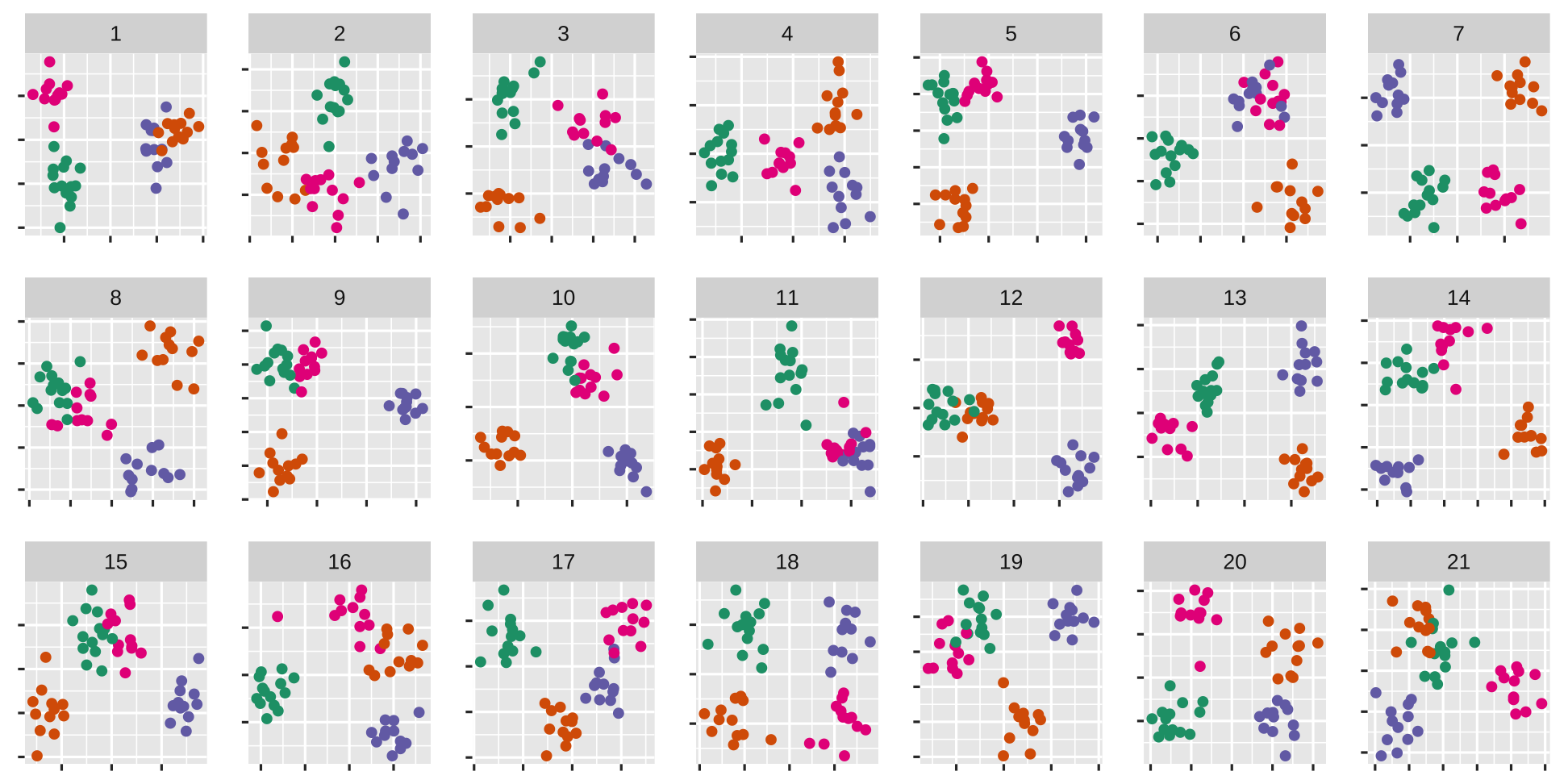
The data plot is

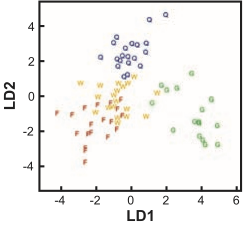
My guess is that nobody picked it?

20 / 45

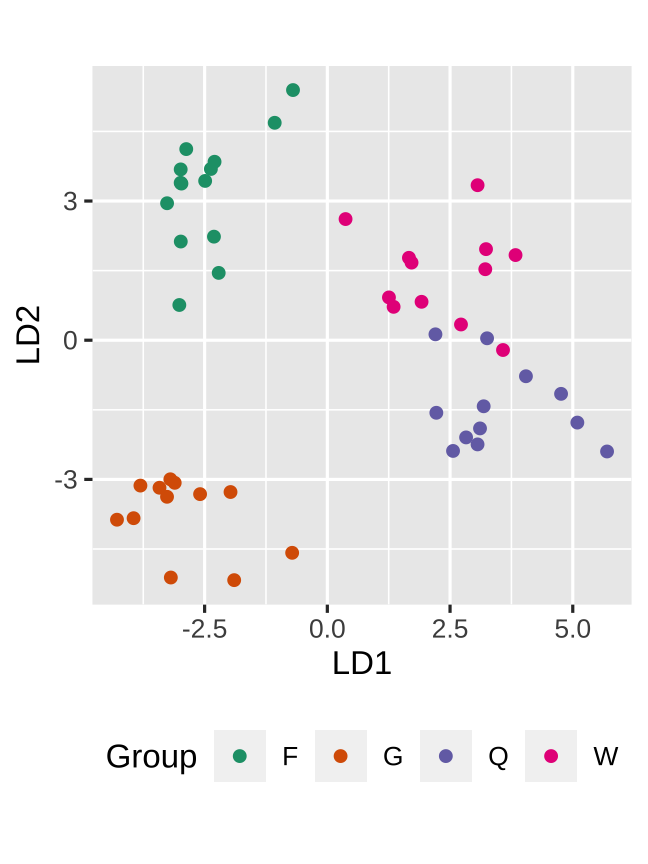
LDA resulted in ... that gynes had the most divergent expression patterns

Toth et al (2010) Proc. of the Royal Society

21 / 45

LDA resulted in ... that gynes had the most divergent expression patterns

Toth et al (2010) Proc. of the Royal Society

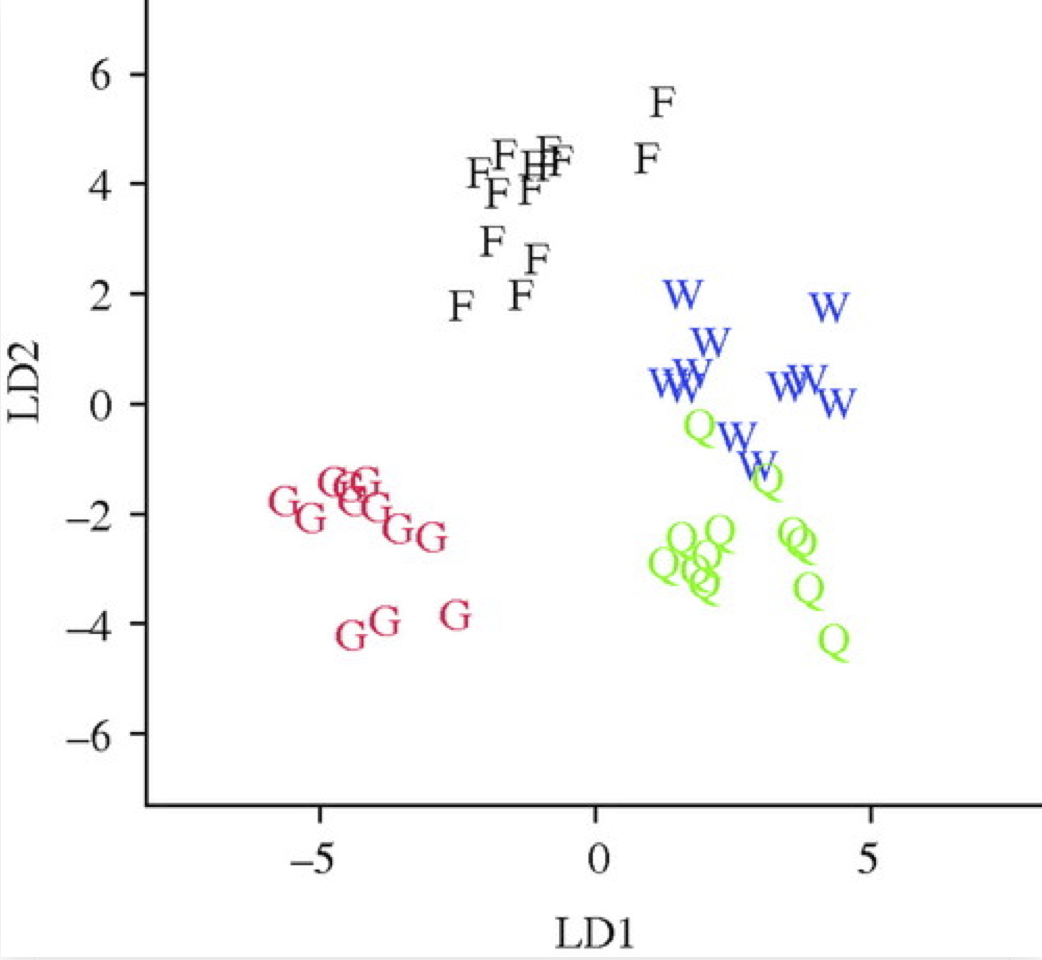
... show that foundress and worker brain profiles are more similar to each other than to the other groups.

Toth et al (2007) Science

21 / 45

True data

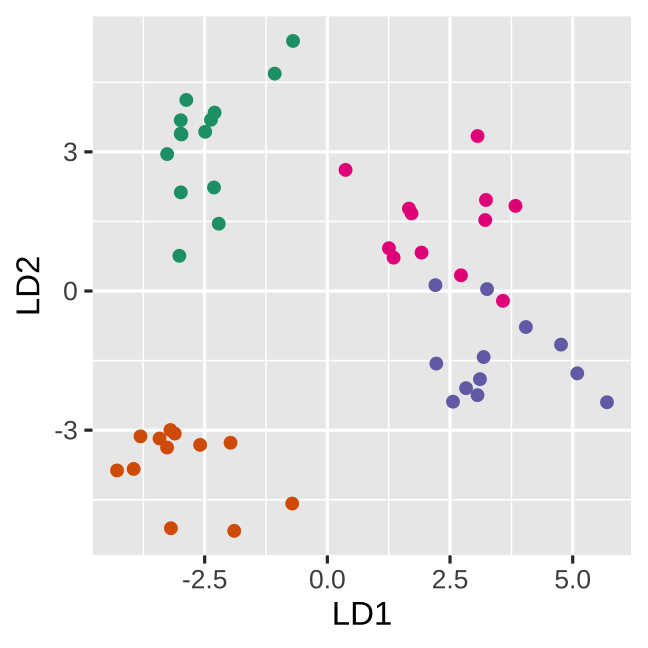
Null data

22 / 45

Space is big, and with few data points, classes can easily be separated

23 / 45

Space is big, and with few data points, classes can easily be separated

spuriously

23 / 45

Space is big, and with few data points, classes can easily be separated

spuriously

The lineup protocol can help people understand the problem

23 / 45

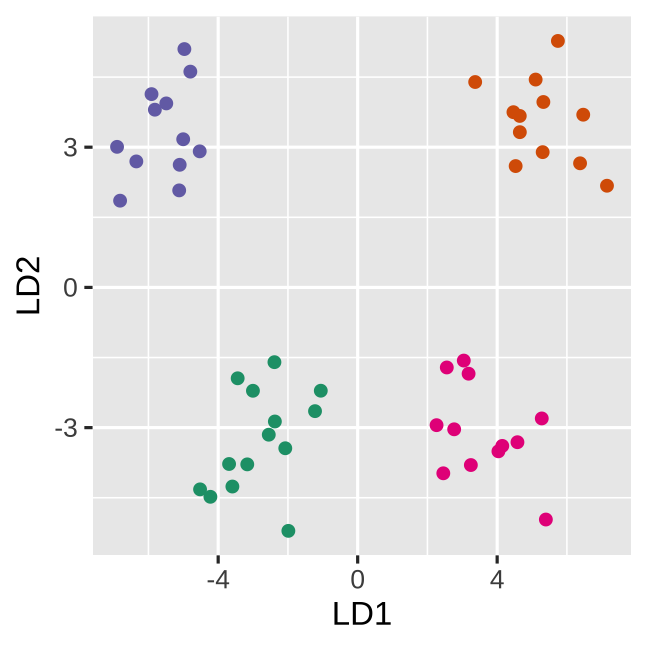
If you first do dimension reduction (e.g. PCA), and then LDA, the problem goes away. LDA into three dimensions shown below.

All data

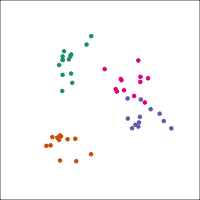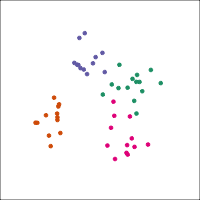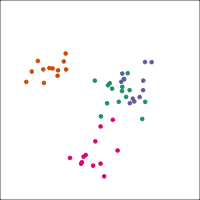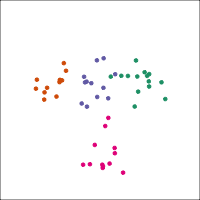
Top 12 PCs

24 / 45

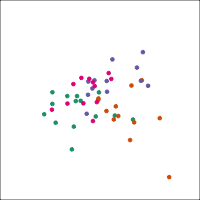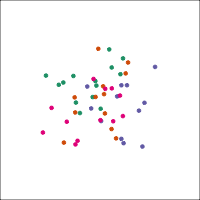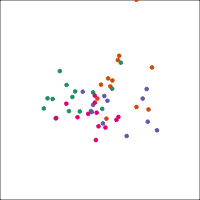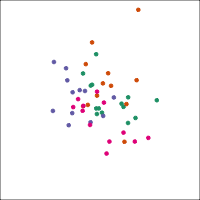
What's that you say? That people can't look at so many plots?25 / 45

What's that you say? That people can't look at so many plots?

Crowd-sourcing can help here

25 / 45

Validation experiment

Majumder et al (2013) conducted validation study to compare the performance of the lineup protocol, assessed by human evaluators, in comparison to the classical test, using subjects employed with Amazon's Mechanical Turk.

26 / 45

Explanation of experiment

Read about it at http://datascience.unomaha.edu/turk/exp2/index.html

$H_{o} : β_{k} = 0 v s H_{a} : β_{k} \neq 0$

70 lineups of size 20 plots:
- $n = 100, 300$
- $β \in [- 6, 4.5]$
- $σ = 5, 12$
351 evaluations by human subjects

27 / 45

Power analysis of human evaluation relative to classical test.

Effect $= \frac{\sqrt{n} \times | β |}{σ}$

Pooling the results from multiple people produces results that mirror the power of the classical test.

28 / 45

High-throughput analysis

😓

The wasps example made us worried about our own RNA-Seq analyses!

29 / 45

Lineup of our own data

I'm going to show you a page of plots

30 / 45

Lineup of our own data

I'm going to show you a page of plots

Each has a number above it, this is its id

30 / 45

Lineup of our own data

I'm going to show you a page of plots

Each has a number above it, this is its id

Choose the plot that you think exhibits the

steepest green line
with relatively small spread of the green points

30 / 45

Lineup of our own data

I'm going to show you a page of plots

Each has a number above it, this is its id

Choose the plot that you think exhibits the

steepest green line
with relatively small spread of the green points

Ready?

30 / 45

31 / 45

Experimental design 2x2 factorial:

Two genotypes (EV, RPA)
Two growing conditions (I, S)
Three reps for each treatment
Approx 60,000 genes

Results from two different procedures, edgeR and DESeq provided conflicting numbers of significant genes, but on the order of 300 significant genes.

One of the top genes was selected for the lineup study, and independent observers engaged through Amazon's Mechanical Turk.

32 / 45

How does a 
 discrepancy 
 happen?33 / 45

Turk results

Is there any significant structure in our data?

34 / 45

Turk results

Is there any significant structure in our data?

24 lineups were made, only one shown to an observer
5 different positions of the data plot
5 different sets of null plots

Pooling results gave a detection rate of 0.65, which is high. There is some structure to our data.

34 / 45

Two aspects of massive multiple testing

ruler on which to measure difference === empirical Bayes
false positives === False Discovery Rate

35 / 45

Two aspects of massive multiple testing

ruler on which to measure difference === empirical Bayes
false positives === False Discovery Rate

Even with these, mistakes can happen, and visualising the data remains valuable

35 / 45

36 / 45

Bring on deep learning, and computer vision models

💻

37 / 45

Monash Masters thesis by Shuofan Zhang

Starting from Majumder's validation study data:

$H_{o} : β_{k} = 0 v s H_{a} : β_{k} \neq 0$

Linear vs no relationship (null)

Training the deep learning model

Same process, but with broader range of parameter settings, and a lot more data!

200,000 samples from each of linear and null scenario generated

$β_{1} \sim \pm U [- 10, - 0.1]$ (linear, null when $β_{1} = 0$ )

$σ \sim U [1, 12]$

$n = U [50, 500]$

38 / 45

Computer model predictionRe-generate the 70 data plots using the same data in Turk study (without null plots)
Use the computer model to predict whether the 70 data plots were "linear" or "null"
The computer model's predicted accuracy over the 70 data plots are recorded as the model's performance.

Human subjects resultsCalculate pp-value associated with each lineup using the binomial formula (from Majumder), with NN=number of evaluations and k=number of people choosing data plot
Draw conclusion: reject the null when the calculated pp-value is smaller than αα.
The accuracy of the conclusions over the 70 lineups 

39 / 45

Repeat of experiment

Using same sample of $n$ , $β$ , $σ$ , new data generated, and images created numerically by binning (to 30x30 pixels), counting and scaling counts to 0-255.

Keras model fitted with 60,000 training images for each class, linear and not.

Accuracy with simulated test data, 93%. Null error 0.0179, linear error 0.1176

Code available in the file keras_correlation.r

40 / 45

Repeat of experiment

Using same sample of $n$ , $β$ , $σ$ , new data generated, and images created numerically by binning (to 30x30 pixels), counting and scaling counts to 0-255.

Keras model fitted with 60,000 training images for each class, linear and not.

Accuracy with simulated test data, 93%. Null error 0.0179, linear error 0.1176

Code available in the file keras_correlation.r Its blindingly fast!

40 / 45

Accuracy

Humans beat computers.

41 / 45

Accuracy

Humans beat computers.

Power analysis

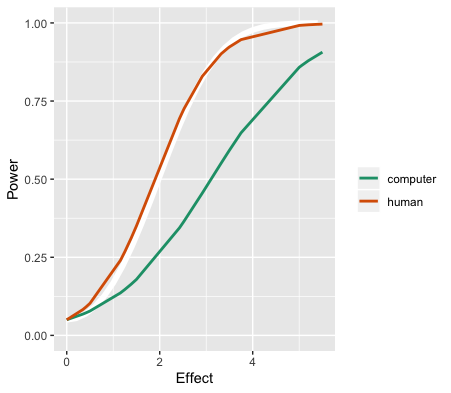
Humans beat computers.

41 / 45

Comparison of human and computer.

		Computer
		Not	Linear
Human	Not	27	0
Human	Linear	15	28

Computer tends to predict too many as "not linear".

42 / 45

Thanks for listening!

Here's what I hope you heard:

Plots can be embedded into an inferential framework
This extends the applicability of statistics to more complex problems
Crowd-sourcing can help mange plot evaluation
Computer vision models are promising ways to scale up

43 / 45

Additional reading

^ Buja et al (2009) Statistical Inference for Exploratory Data Analysis and Model Diagnostics, RSPT A
^ Wickham et al (2010) Graphical Inference for Infovis, TVCG
^ Hofmann et al (2012) Graphical Tests for Power Comparison of Competing Design, TVCG
^ Majumder et al (2013) Validation of Visual Statistical Inference, Applied to Linear Models, JASA
^ Yin et al (2013) Visual Mining Methods for RNA-Seq data: Examining Data structure, Understanding Dispersion estimation and Significance Testing, JDMGP
^ Zhao, et al (2014) Mind Reading: Using An Eye-tracker To See How People Are Looking At Lineups, IJITA
^ Lin et al (2015) Does host-plant diversity explain species richness in insects? Ecological Entomology
^ Roy Chowdhury et al (2015) Using Visual Statistical Inference to Better Understand Random Class Separations in High Dimension, Low Sample Size Data
^ Loy et al (2017) Model Choice and Diagnostics for Linear, CS
Mixed-Effects Models Using Statistics on Street Corners, JCGS
^ Roy Chowdhury et al (2018) Measuring Lineup Difficulty By Matching Distance Metrics with Subject Choices in Crowd- Sourced Data, JCGS

44 / 45

Acknowledgements

Slides created via the R package xaringan, with iris theme created from xaringanthemer.

The chakra comes from remark.js, knitr, and R Markdown.

Slides are available at https://dicook.org/files/vISEC2020/slides.html and supporting files at https://github.com/dicook/vISEC2020.

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Image credit: Di Cook, 2019

45 / 45

Help

Keyboard shortcuts

↑, ←, Pg Up, k

Go to previous slide

↓, →, Pg Dn, Space, j

Go to next slide

Home

Go to first slide

End

Go to last slide

Number + Return

Go to specific slide

b / m / f

Toggle blackout / mirrored / fullscreen mode

Clone slideshow

Toggle presenter mode

Restart the presentation timer

?, h

Toggle this help

Making inference using data plots, with application to ecological statistics

Di Cook Monash University

vISEC June 24, 2020

Data plots are utilised widely in ecology, often to make decisions. They can and should be integrated into the classical statistics infrastructure.

Inference for data plots requires

Inference for data plots requires

Inference for data plots requires

Inference for data plots requires

Inference for data plots requires

Why is a plot a statistic?

Why is a plot a statistic?

Null generating mechanism: Example 1

Null generating mechanism: Example 1

Null generating mechanism: Example 2

Null generating mechanism: Example 2

Pretend you haven't seen the data plot

In each case, the data plot was identifiable, and the null hypothesis would be rejected

Inference for graphics infrastructure

Visual inference broadens the scope of statistics

Let's do a real lineup test

Lineup protocol

Lineup protocol

Lineup protocol

Lineup protocol

Lineup protocol

What's that you say? That people can't look at so many plots?

What's that you say? That people can't look at so many plots?

Validation experiment

Explanation of experiment

High-throughput analysis

Lineup of our own data

Lineup of our own data

Lineup of our own data

Lineup of our own data

How does a discrepancy happen?

Turk results

Turk results

Bring on deep learning, and computer vision models

Training the deep learning model

Computer model prediction

Human subjects results

Repeat of experiment

Repeat of experiment

Accuracy

Accuracy

Power analysis

Comparison of human and computer.

Thanks for listening!

Additional reading

Acknowledgements

Data plots are utilised widely in ecology, often to make decisions. They can and should be integrated into the classical statistics infrastructure.

Help

Di Cook
Monash University

vISEC
June 24, 2020

How does a
discrepancy
happen?